La relation pression-volume
Pour ceux qui ont raté le début, j’ai le privilège et l’honneur de publier sur ce blog des articles synthétisant les bases de la physiologie cardiaque, rédigées par l’incomparable Dr Abassade. Ces notions sont utiles (voire indispensables) à l’interprétation de nos échos en fonction de la situations hémodynamique du patient.
Thème du jour : Harry Potter et la chambre ventriculaire
Enjoy.
Merci Philippe!
CHAPITRE IV : LA CHAMBRE VENTRICULAIRE
LA RELATION PRESSION VOLUME
C’est Otto FRANK le premier, en 1898, qui a présenté la contraction cardiaque sous la forme d’une boucle dans un plan défini par la pression en ordonnées, et le volume en abscisse.
Dans les années 1960 Monroe, puis surtout à partir de 1974 avec les travaux de Suga et Sagawa, cette « nouvelle » façon de représenter le cycle cardiaque a bénéficié d’un important succès, pour plusieurs raisons :
1) La description du cycle cardiaque se fait à partir de la chambre ventriculaire et non plus à partir de la fibre isolée, elle devient plus accessible que la représentation tri dimensionnelle.
2) Ces boucles donnent une représentation graphique du volume d’éjection systolique et du travail cardiaque, paramètres dont l’importance clinique est grande.
3) Des points remarquables sont définis : le point de coordonnées (PTS ; VTS) point qui « résume » la systole, le point de coordonnées (PTD ; VTD), point qui « résume » la diastole.
4) Ces courbes permettent de redéfinir l’inotropie, grâce à la relation ETS = PTS/VTS, relation « phénoménologique » selon Sagawa.
5) La diastole est décrite. Par la mesure simultanée de la pression et du volume il va être possible d’étudier leur variation et des indices de la fonction muscle en diastole.
6) Il est possible en construisant des familles de courbes, de montrer les effets sur un même cœur des variations de la charge ou de la contractilité à la fois sur la systole et sur la diastole.
7) Il est également possible de visualiser les effets hémodynamiques d’une intervention pharmacologique.
8) enfin à partir de la relation Pression Volume de la chambre, sera définie une relation Pression artérielle Volume d’éjection, l’Elastance artérielle, témoin des propriétés physiques de l’arbre artériel. La notion de post charge est élargie et un nouveau champ d’étude est ouvert: le couplage aorte VG.
1. LA RELATION PRESSION VOLUME EN SYSTOLE (28, 29, 30)
A. Description
Pour obtenir cette boucle il est nécessaire de recueillir en même temps la pression par un micro manomètre mis en place dans le ventricule, et le volume par ciné angiocardiographie.
A partir du point A point de coordonnées (VTD ; PTD), débute la contraction. C’est la phase isovolumétrique qui amène la courbe jusqu’au point B, ouverture des sigmoïdes.
Débute alors l’éjection ventriculaire rapide alors que la pression continue d’augmenter, puis lorsque la contraction s’arrête commence à diminuer jusqu’au point C de coordonnées (VTS; PTS).
La courbe ensuite voit la pression chuter rapidement pendant la phase de relaxation iso volumétrique, jusqu’au point D, où la valve auriculo ventriculaire s’ouvre.
De D à A se produit le remplissage diastolique, la pente de la partie DA traduit la compliance générale de la chambre, résultante de la relaxation, phénomène actif qui a démarré dès le début de la chute de pression, et de la rigidité de la chambre (distensibilité passive) du ventricule dans la seconde partie du remplissage diastolique.
Le volume d’éjection systolique (VES) est représenté par la distance séparant VTD de VTS. La fraction d’éjection FE est le rapport entre le VES et le VTD : FE = VES/VTD = 0.6
Le travail cardiaque est représenté par la surface délimitée par la courbe.
Figure 1 : Courbe Pression Volume
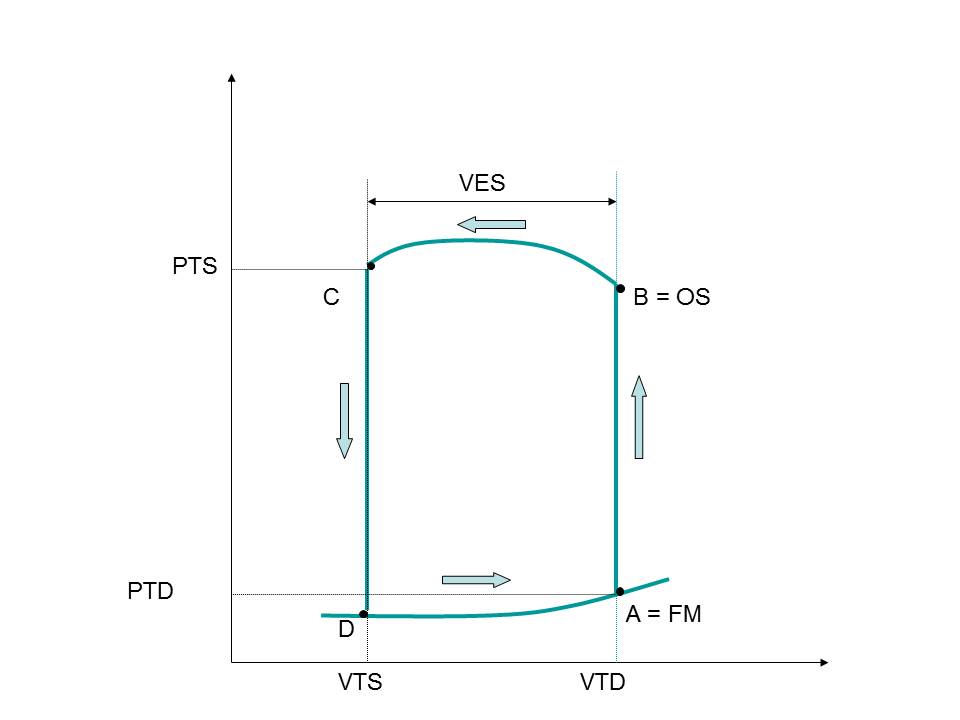
B. La relation Pression télésystolique, Volume télésystolique
Lorsque on fait varier la post charge, on s’aperçoit qu’il existe une relation entre le VTS et la PTS : plus la PTS est élevée et plus le VTS est élevé.
Pour un état contractile donné, les VTS obtenus selon les différentes PTS, vont se répartir sur une droite ETS ou droite de l’élastance télésystolique ou élastance maximale représentative de cet état contractile. Cette droite va couper l’axe des volumes à distance de l’origine en un point appelé Vd.
Figure 2 : Courbes PV en faisant varier la post charge (à gauche), la précharge (à droite)
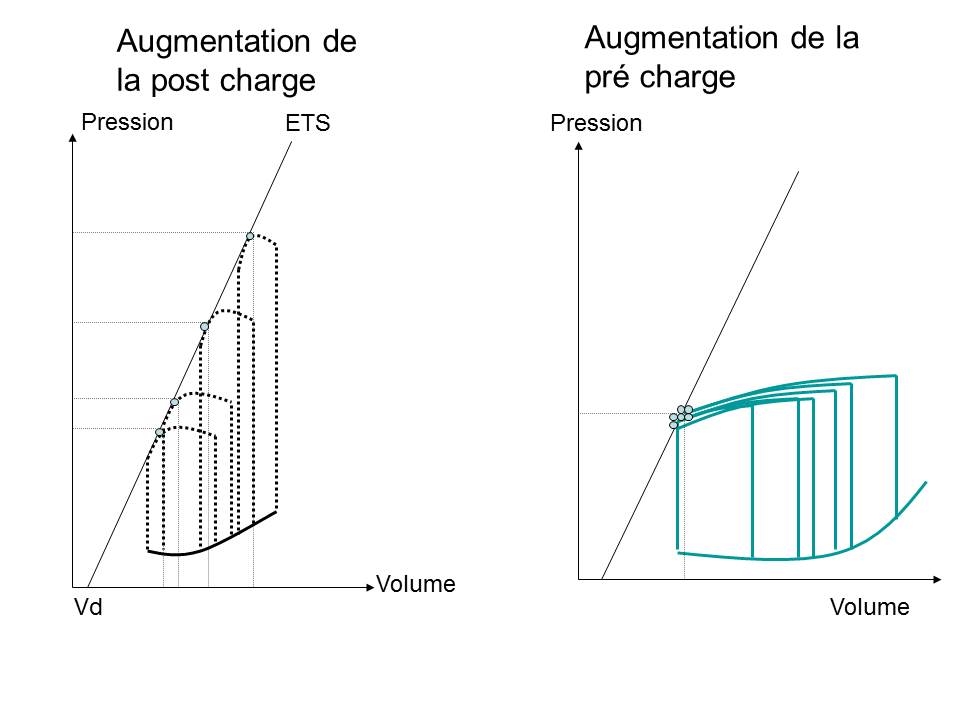
Le volume télésystolique est une fonction linéaire croissante de la pression télésystolique : Le rapport entre la PTS et le VTS est constant.
Cette relation entre PTS et VTS peut s’écrire : PTS = ETS (VTS – Vd), ou ETS est la pente de la droite unissant tous les points de coordonnées (PTS ; VTS), Vd l’interception de cette droite avec l’axe des volumes ou volume résiduel.
En re arrangeant cette équation il va être possible d’exprimer le volume d’éjection systolique (VES), en fonction de la PTS :
VES = VTD – (Vd + PTS/ETS).
Cette équation prédit que pour un état contractile donné, et une précharge donnée (VTD) le volume d’éjection systolique et la fraction d’éjection (VES/VTD) seront d’autant plus réduits que la pression télésystolique est grande.
En d’autres termes c’est le niveau de la pression télésystolique qui détermine le volume d’éjection systolique (pour un état contractile et un volume initial donnés).
C. Effet de l’inotropie sur la relation PTS VTS
L’augmentation de la contractilité augmente la pente de la droite ETS de la relation PTS/VTS sans changer Vd (28, 29).
Figure 3 : Effet de l’inotropie sur la relation PTS/VTS : voir texte
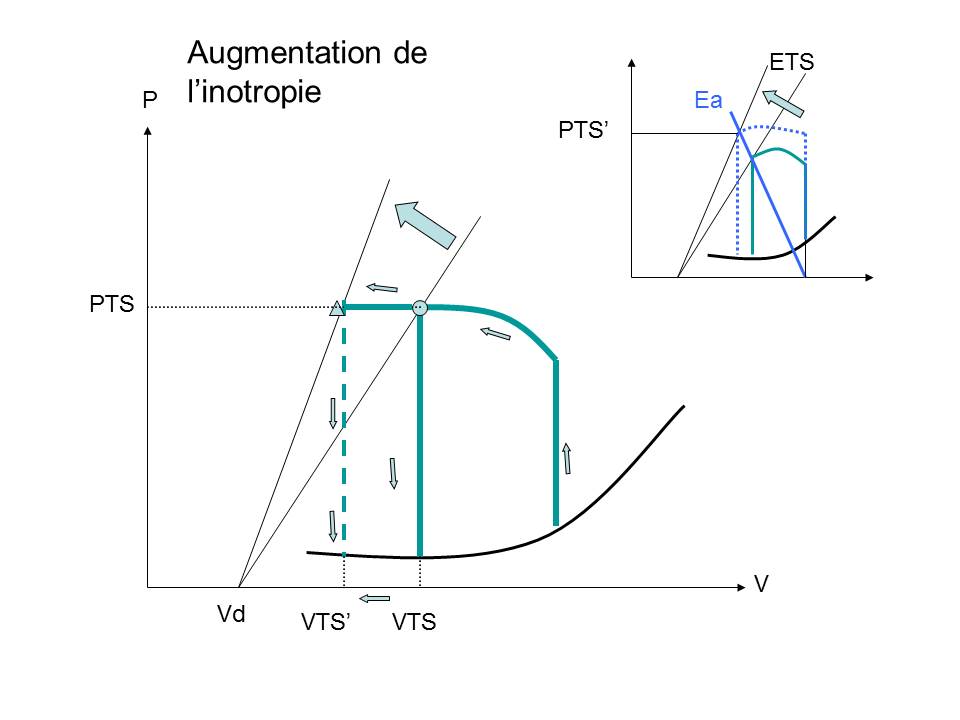
On peut visualiser sur la courbe l’effet de l’augmentation de l’inotropie : le volume d’éjection et le travail cardiaque augmentent pour une même pression télésystolique développée. Ceci est en accord avec l’effet de l’inotropie sur la relation force vitesse : la vitesse de raccourcissement est plus élevée à force égale (cf chapitre 2). Cela implique (si le temps d’éjection est le même) que la longueur finale sera plus courte. Le VTS sera donc plus petit et le VES et la FE seront plus grands.
En fait, il y aura nécessairement une augmentation de la PTS, si le VES augmente, du fait de propriétés du système artériel. Nous le verrons au chapitre IV. (Figure 3 courbe du haut)
2. LA RELATION PRESSION VOLUME EN DIASTOLE (3, 4, 16, 31, 32)
La relation pression volume va décrire la diastole de manière globale alors qu’elle dépend de nombreux facteurs. La courbe pression volume est la somme de ces influences, le point (PTD ; VTD) un résumé de cette courbe.
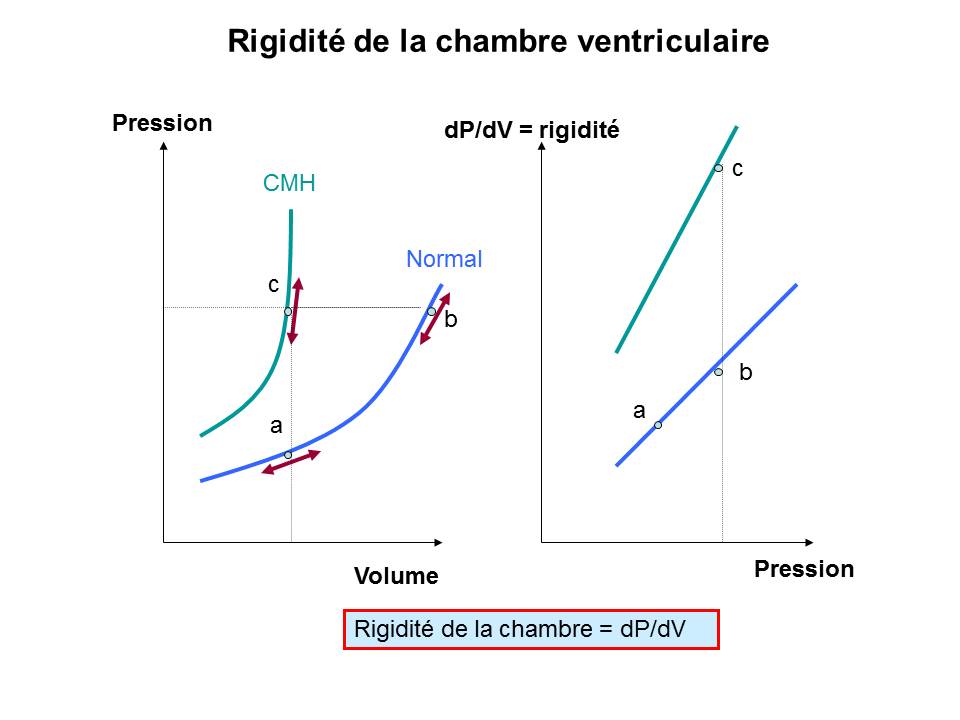
A. La rigidité de la chambre.
Elle est définie comme la variation de pression par rapport à la variation de volume (dP/dV).
La courbe pression volume en diastole est de type exponentiel, ce qui implique que plus la pression et le volume sont élevés plus cette rigidité s’accroît (Figure 5).
Toutefois pour de faibles niveaux de pression cette relation est linéaire, et pour de hauts niveaux elle est sigmoïde (3, 4)
Cette loi exponentielle reflète les propriétés passives du myocarde qui se comporte, ainsi que la plupart des tissus biologiques, comme un matériau non hookien. Dans la loi de Hooke, la relation entre le volume et la pression de distension est linéaire et la rigidité (la dérivée) constante.
La relation pression volume du myocarde exponentielle est de formule :
P = A eKc.V : P est la pression, V le volume, Kc la constante, A la pression au volume zéro.
De ce fait la rigidité (la dérivée) augmente au fur et à mesure de l’augmentation de la pression de distension.
En revanche la relation dP/dV en fonction de P est linéaire : dP/dV = Kc P (Figure 4).
Figure 4 :
A gauche : relation Pression Volume en diastole normale et dans une CMH.
A droite : rigidité en fonction de la pression, constante Kc. Voir texte.
La pente Kc de cette relation pourrait apparaître comme une constante simple de la rigidité de la chambre. Cependant pour différentes raisons (la relation PV est mieux décrite par une exponentielle à 3 constantes, le coefficient Kc a une dimension (31)), Kc ne semble pas être un indice fiable.
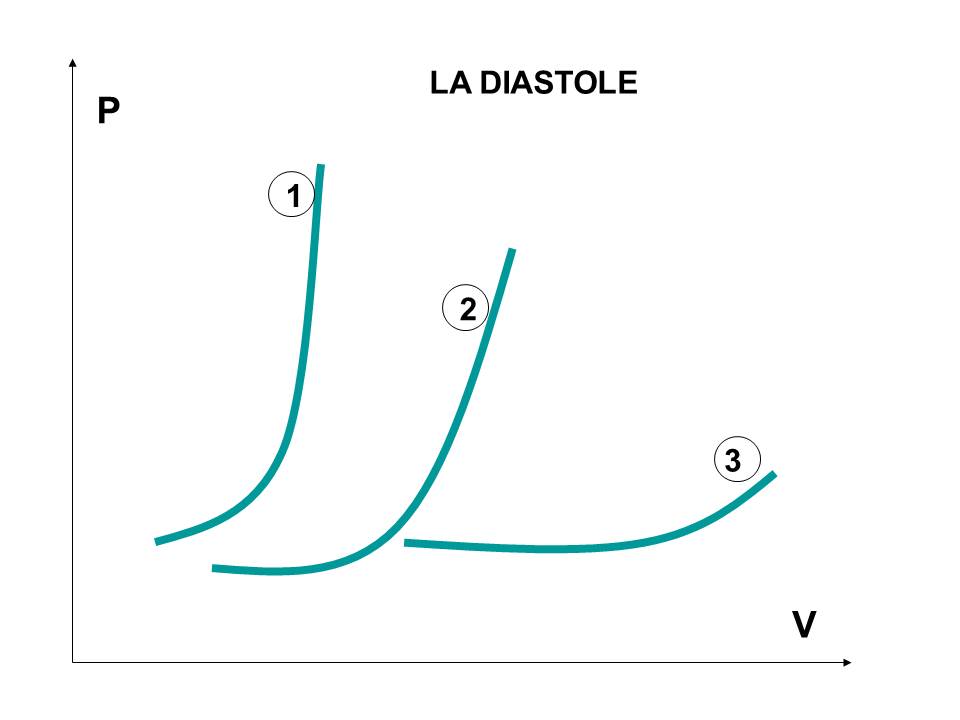
La relation dP/dV est elle idéale pour comparer la rigidité de la chambre de deux ventricules différents ? (Figure 5)
Figure 5 : courbe PV diastolique pour une CMH (1) un sujet normal (2), une cardiopathie dilatée (3).
Ainsi chez un sujet porteur d’une cardiomyopathie hypertrophique (CMH) par exemple, la relation pression volume est déviée vers la gauche : à chaque niveau de volume correspondra une pression de remplissage plus élevée que chez un sujet normal (33).
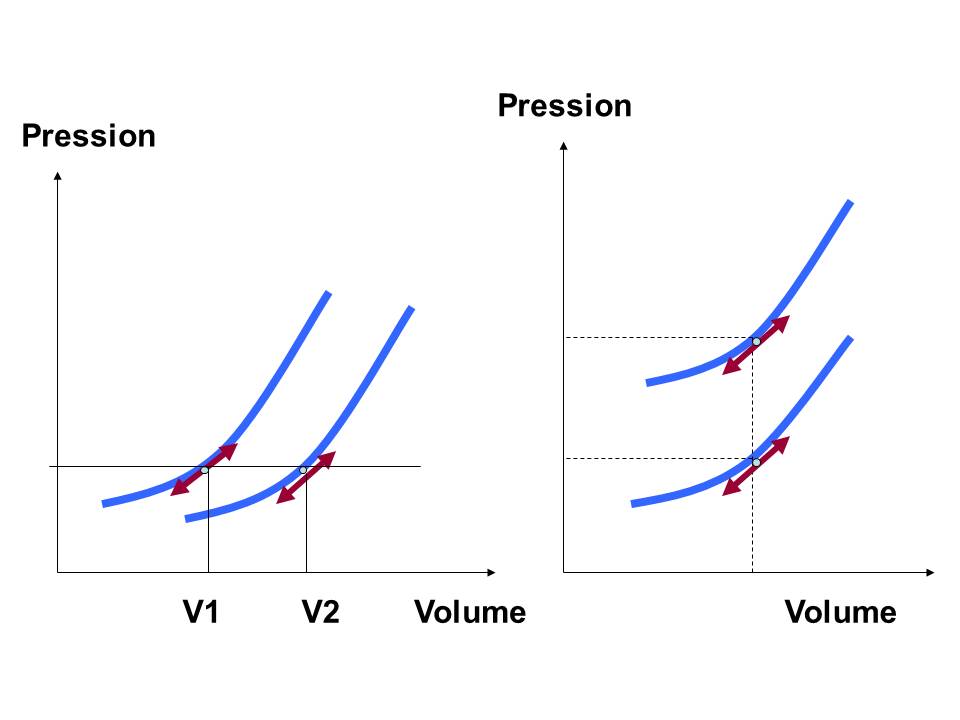
En fait la relation dP/dV n’est pas suffisante pour séparer deux ventricules de comportement diastolique différent (Figure 6) :
En effet lors de la survenue brutale d’un épanchement péricardique par exemple, la courbe Pression Volume est déviée vers le haut. La pente est identique, suggérant une rigidité de la chambre identique, pourtant la pression de remplissage à volume égal est augmentée : Il est donc important de considérer dP/dV mais également la position de la courbe par rapport au zéro de référence. (16)
Il est également théoriquement possible que la courbe soit déviée à droite, sans que la rigidité ne change : à chaque niveau de pression correspondra la même pente dP/dV. Il apparaît préférable donc d’utiliser la rigidité volumique (« volume elasticity »), qui sera plus discriminante (31) : la figure 7 (à gauche) illustre la différence entre la rigidité volumique V1dP/V, et la rigidité volumique V2 dP/dV.
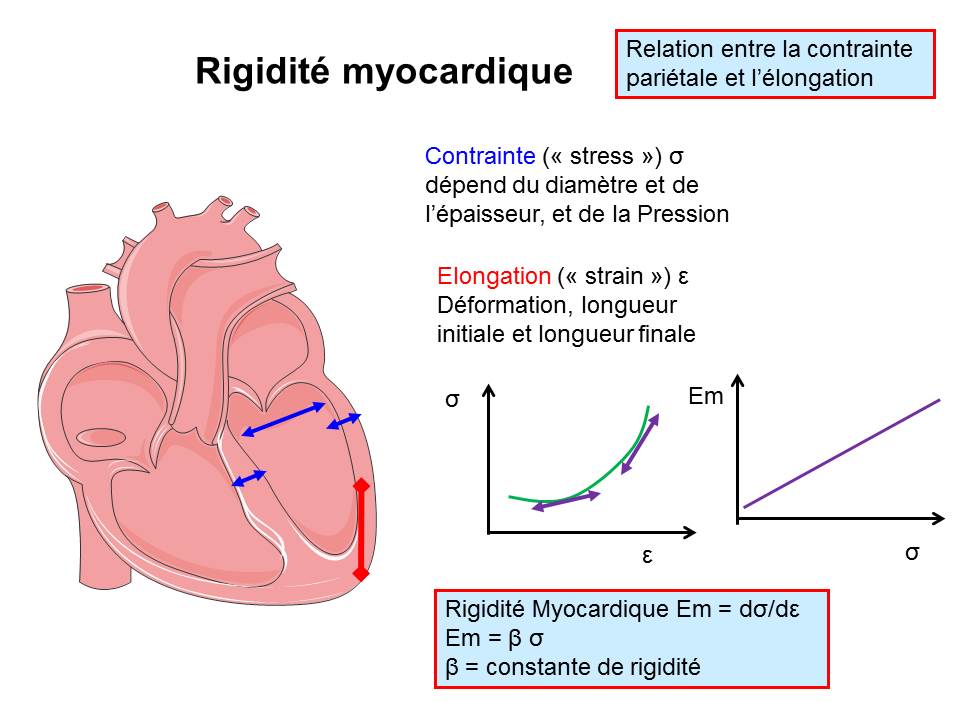
B. La rigidité myocardique.
L’augmentation de la pression au cours de la diastole sera dépendante aussi de caractéristique intrinsèque du myocarde appelée rigidité élastique du myocarde (2, 3, 4, 16, 32): Si la rigidité de la chambre explore la capacité du ventricule gauche à se laisser distendre passivement lors du remplissage, la rigidité myocardique explore le muscle lui même, et sa capacité à résister à une force d’élongation.
Les grandeurs étudiées vont donc prendre en compte des propriétés propres du muscle comme la contrainte pariétale (« stress ») qui fait intervenir pression, diamètre et épaisseur (cf chapitre 2), et sa relation avec l’élongation ou déformation (« strain »).
Les notions de Mécanique des milieux continus vont pouvoir s’appliquer :
L’élongation ε est définie comme : ε = l-l0 /l0
Où l0 est la longueur initiale du muscle à charge nulle, l la longueur finale. Cette élongation sera représentée dans un système dit « Lagrangien » car l’unité élémentaire qui est décrite (un segment de myocarde) est suivie dans son mouvement, en prenant pour référentiel sa position de départ (l0) et non un zéro de référence.
Comme nous l’avons vu pour la rigidité de la chambre où la relation Pression Volume est exponentielle, la relation entre la contrainte pariétale et l’élongation est également exponentielle et non linéaire contrairement à la loi de Hooke (rappelons que les matériaux biologiques sont « non hookiens ».)
Cette relation stress/strain s’écrit : σ = ά(eβε – 1).
σ est la contrainte pariétale, ά une constante, β la constante de rigidité (ou module d’élasticité) myocardique, ε est l’élongation.
Figure 7 :
Et de la même façon que la rigidité de la chambre était la dérivée dP/dV, la rigidité (ou élasticité) myocardique Em est égale à la variation de la contrainte en fonction de la variation de l’élongation : Em = dσ/dε.
Là encore, la relation dσ/dε en fonction de σ est linéaire. Em = β σ, β étant la constante de rigidité myocardique (que certains (3,4) appellent k, ce qui amène une confusion).
C. Intérêts et limites
a). La rigidité
L’analyse de la rigidité fait appel à des calculs complexes et repose sur des hypothèses très précises (32) : le VG est une sphère d’épaisseur constante, toutes les fibres supportent la même contrainte que les fibres à mi paroi, le système est en équilibre statique, la pression cavitaire est égale à la charge, le muscle a un comportement élastique.
Du fait de ces importantes réserves méthodologiques des indices simplifiés, dont l’utilisation est satisfaisante (3, 4, 16, 32), sont plus couramment employés. Ces indices utilisent le volume de la chambre (V), le volume de la paroi (Vw), ou encore plus simple le rapport épaisseur sur rayon (e/r).
En effet le volume de la chambre, l’épaisseur de la paroi puis la constante de rigidité myocardique β sont dans cet ordre, les trois grandeurs principales qui déterminent la courbe Pression / Volume en diastole selon des modèles théoriques (32).
Autrement dit la rigidité myocardique intervient de façon moindre que le volume et l’épaisseur, dans les conditions physiologiques.
Figure 8
Au total, la courbe pression volume permet de décrire le remplissage diastolique, le point VTD, PTD est le point résultant de tous ces mécanismes. L’ensemble des phénomènes pendant la diastole est cependant incomplètement décrit par cette seule relation.
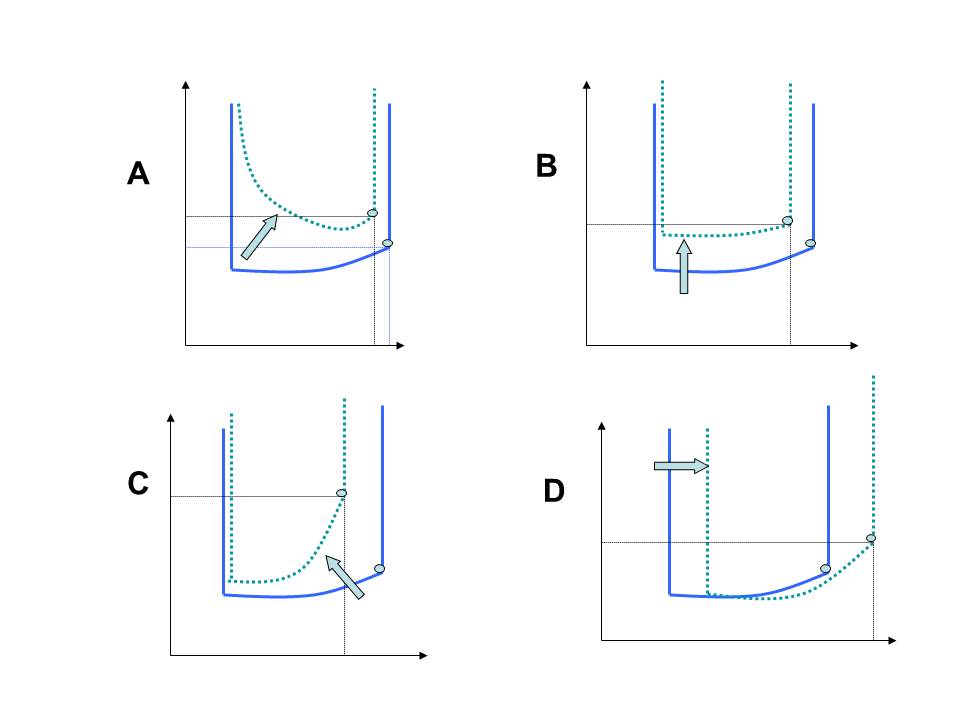
La figure 8 offre des exemples de modifications théoriques de la courbe pression volume :
A : effet d’un trouble de la relaxation qui affecte la partie initiale de la diastole.
B : épanchement péricardique.
C : augmentation de la rigidité intrinsèque myocardique (hémochromatose par exemple).
D : effet d’une dilatation du VG.
b). La déformation (le strain)
L’analyse de la déformation du myocarde a, en revanche, trouvé des applications nouvelles : Elle est étudiée par l’échographie (2D strain) grâce à la technique du « speckle tracking ». Il est possible de quantifier la déformation du myocarde dans trois directions, longitudinale (plus en rapport avec le raccourcissement des fibres sous endocardiques dont la direction générale favorise ce mouvement), radiale (la fraction d’éjection explore ce mouvement) et circonférentielle. Enfin la torsion de la base du cœur par rapport à la pointe est la combinaison de ces trois mouvements élémentaires.
Le strain longitudinal régional et global est mesuré de façon courante ; il permet l’analyse d’un mouvement cardiaque jusque-là mal décrit, et apporte des informations supplémentaires sur la contraction myocardique et la relaxation.
3. IMPLICATIONS CLINIQUES (16, 34)
A. Modification de la courbe en cas d’insuffisance cardiaque congestive
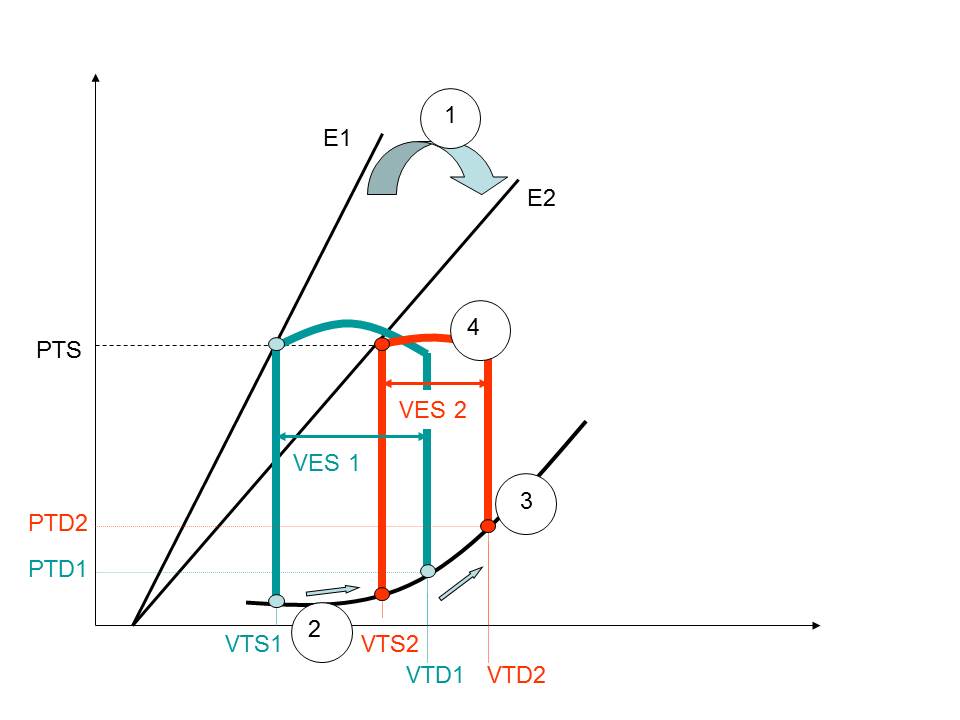
En cas d’insuffisance cardiaque, le premier événement est la baisse de la contractilité qui se traduit par une diminution de la pente de la droite d’élastance ETS (E1), sans changer d’origine, conduisant à une nouvelle droite E2, témoin d’une autre relation PTS / VTS. (1)
Si la PTS ne change pas, le volume télésystolique ventriculaire G augmente (VTS1 versus VTS 2) (2), ce qui implique que le remplissage se fait en empruntant la partie ascendante de la courbe pression / volume diastolique (ou élastance passive). La PTD VG va augmenter (PTD 1 versus PTD2), ainsi que le VTD (3).
Le volume d’éjection systolique va diminuer (VES 1 versus VES 2) (4).
Il apparaît sur la boucle pression / volume toutes les modifications de l’insuffisance cardiaque à FE basse : diminution de la contractilité (1), augmentation de la taille de la cavité (2), augmentation des pressions de remplissage (3), diminution du volume d’éjection systolique (4).
Figure 9
Modifications liées à l’insuffisance cardiaque à FE basse
B. Effet d’un vasodilatateur sur la courbe pression volume d’une insuffisance cardiaque à FE basse
L’intervention d’un vaso-dilatateur sur la courbe Pression volume telle qu’elle a été transformée lors d’une baisse de la contractilité (cf supra), va améliorer les conditions de fonctionnement de la pompe (Figure 10).
Figure 10
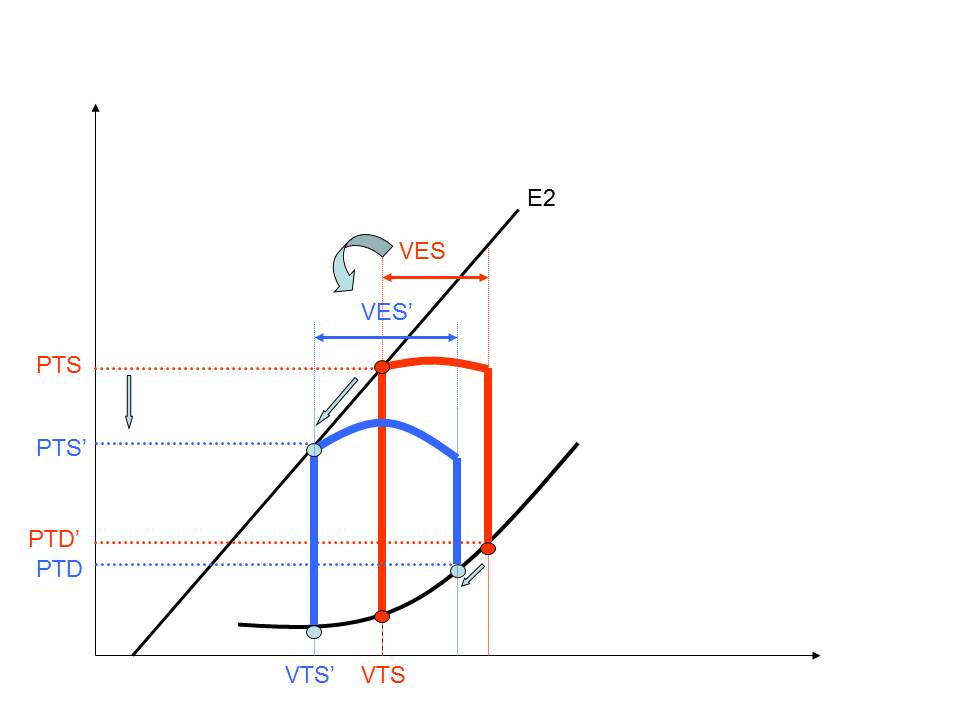
La prescription d’un vasodilatateur type IEC, va diminuer la PTS, et de ce fait diminuer le VTS (qui devient VTS’), du fait de la constance du rapport PTS /VTS.
Le remplissage se fera sur la portion horizontale de la courbe PV en diastole, ce qui diminuera les pressions de remplissage (PTD’ versus PTD) et augmentera le volume d’éjection systolique (VES’ versus VES).
Magnifique as usual, chers internes interro dans 2 mois avant de passer à Brustaert
Merci!
Je transmets les compliments à l’auteur!
Je ne dit rien sur le strain avant de réviser la math sup PT et la L3 d’électronique
c’est très courageux de publier ça fin juillet
J’ai peur que les gens s’ennuient à la plage 😉
Où puis-je trouver les références ?
A quoi ressemblerai la courbe suite à l’introduction de diurétique sur une insuffisance cardiaque congestive ou choc cardiogenic?